Úvod
Vzhledem k rostoucímu počtu obyvatelstva a se zvyšující se spotřebou energie vzniká otázka, jak řešit zásobování energií a při tom se vyhnout negativnímu vlivu na životní prostředí. Spalování fosilních paliv přináší řadu problémů se znečišťováním planety; roste zároveň koncentrace oxidu uhličitého a v důsledku skleníkového efektu se postupně Země otepluje. K řešení už nyní přispívají obnovitelné zdroje, mezi nimi zaujímá důležité místo přímá přeměna energie slunečního záření na energii elektrickou. Slunce představuje prakticky nevyčerpatelný zdroj a jeho využití neznamená skleníkový efekt ani tepelné zamoření. Sluneční záření má však nízkou hustotu zářivého toku (v České republice přibližně 1 kW/m2 na povrchu Země), jeho velikost závisí na počasí a je omezeno na denní dobu, s čímž souvisí nutnost akumulace energie. Zářivý tok, který Slunce vysílá na celou Zemi je 175 000 TW, což je o mnoho řádů více než je spotřeba lidstva, jak vyplývá z výpočtu na základě údajů v [1]. I z tohoto hlediska je využívání sluneční energie perspektivní.
Sluneční záření
Elektromagnetické záření, které vysílá Slunce, se příliš neliší od záření černého tělesa při teplotě 6000 K. Celkový zářivý tok na jednotku plochy ve střední vzdálenosti Země–Slunce mimo zemskou atmosféru udává solární konstanta, která má hodnotu 1,353 kW/m2. Toto záření označované jako AM 0, se při průchodu vzduchem oslabuje a mění se i jeho spektrální složení. Je-li Slunce v zenitu, procházejí jeho paprsky minimální tloušťkou zemské atmosféry a odpovídající záření je AM 1. Nejpoužívanějším zářivým tokem pro testování slunečních článků je standard AM 1,5 s plošnou hustotou výkonu 1 kW/m2 (viz Obr. 1).
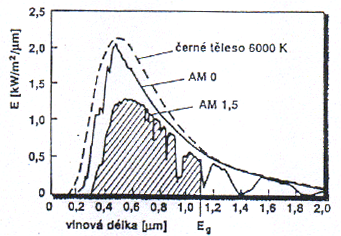
Absorpční pásy ve spektru AM 1,5 jsou způsobeny hlavně absorpcí vodními parami, oxidem uhličitým a kyslíkem. Průchodem atmosférou se celkově zeslabuje sluneční záření asi o 30 %. Sluneční záření na povrchu Země obsahuje také difúzní složku, která vzniká jeho rozptylem v atmosféře. Za jasného dne činí 10–20 % celkové intenzity, ale s přibývající oblačností jeho podíl roste.
Princip činnosti slunečního článku
Fotovoltaické články jsou polovodičové součástky, které přeměňují energii záření na energii elektrickou. Je-li v polovodiči absorbován foton s dostatečnou energií, vybudí elektron z valenčního do vodivostního pásu a vznikne pár elektron-díra. Vnitřní elektrické pole v článku páry rozdělí a ve vnějším obvodu se objeví elektrický proud. K rozdělení páru slouží nejčastěji pole vytvořené přechodem PN. Přitom se využívají jak homogenní, tak heterogenní přechody i složitější struktury, které vznikají jako jejich kombinace.
Pravděpodobnost absorpce fotonů je charakterizována absorpčním koeficientem $K(\lambda)$, kde $\lambda$ je vlnová délka. Dále se zavádí kvantový výtěžek $\beta(\lambda)$, který udává průměrný počet párů elektron-díra vznikajících při absorpci jednoho fotonu.
Teorie fotovoltaických článků
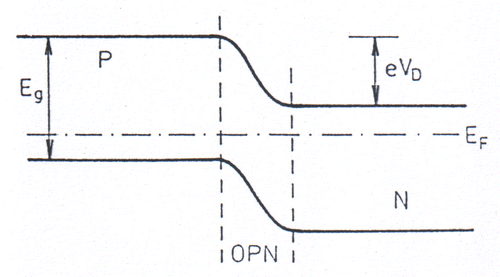
Budeme se zde zabývat základním případem článku na bázi homogenního přechodu PN (viz Obr. 2) a naznačíme výpočet světlem generovaného proudu. Světlo dopadá ze strany polovodiče typu P a obecně se může absorbovat v části P, v oblasti prostorového náboje (OPN) a části N. Nosiče náboje, které se generují v neutrálních částech, se buď dostanou difúzí do OPN a jsou rozděleny elektrickým polem, nebo před dosažením této oblasti rekombinují a nepřispívají k fotoproudu. Nosiče vytvořené v OPN jsou ihned rozděleny polem, a proto se obvykle předpokládá jejich dokonalý příspěvek k proudu.
Chování nosičů náboje se popisuje soustavou diferenciálních rovnic, které tvoří transportní rovnice pro hustotu elektronového a děrového proudu \begin{equation} \label{J_n} J_n = e \mu_n n E + e D_n \frac{\mathrm{d}n}{\mathrm{d}x} \end{equation} \begin{equation} \label{J_p} J_p = e \mu_p p E - e D_p \frac{\mathrm{d}p}{\mathrm{d}x}, \end{equation} kde $n$ a $p$ jsou koncentrace elektronů a děr, $n_0$ a $p_0$ jsou rovnovážné koncentrace nezávislé na souřadnici, $\Delta n$ a $\Delta p$ jsou koncentrace generované světlem, přičemž platí $n = n_0 + \Delta n$ a $p = p_0 + \Delta p$, a dále rovnice kontinuity \begin{equation} \label{kont_n} \frac{\partial n}{\partial t} = G_n - \frac{\Delta n}{\tau_n} + \frac{1}{e} \frac{\mathrm{d}J_n}{\mathrm{d}x} \end{equation} \begin{equation} \label{kont_p} \frac{\partial p}{\partial t} = G_p - \frac{\Delta p}{\tau_p} - \frac{1}{e} \frac{\mathrm{d}J_p}{\mathrm{d}x}, \end{equation} kde $e$ je náboj elektronu, $\mu_n$ a $\mu_p$ jsou pohyblivosti elektronů a děr, $D_n$ a $D_p$ jsou příslušné difúzní koeficienty, $\tau_n$ $\tau_p$ doby života, $G_n$ a $G_p$ rychlosti generace nosičů náboje a $E$ je elektrické pole.
Výpočet proudu naznačíme pro jednorozměrný případ a monochromatické záření a označíme ještě difúzní délky minoritních nosičů $L_n$ a $L_p$.
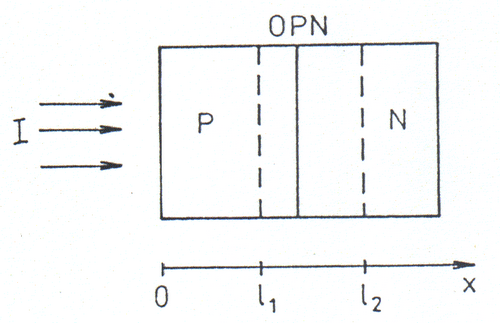
Zabývejme se nejprve příspěvkem minoritních nosičů k proudu z části typu P mimo OPN, kde nepůsobí elektrické pole (viz Obr. 3). Ve stacionárním případě lze použitím rovnic $\eqref{J_n}$ a $\eqref{kont_n}$ psát \begin{equation} \label{D_n} D_n \frac{\mathrm{d}^2 \Delta n}{\mathrm{d}x^2} - \frac{\Delta n}{\tau_n} = -G_n. \end{equation} Generace elektronů při zanedbání odrazu světla, které je charakterizováno plošnou hustotou fotonového toku $I$ ($[I] = \mathrm{cm^{-2}s^{-1}}$) je \begin{equation} G_n = \beta K I \exp(-Kx). \end{equation} Po dosazení do rovnice $\eqref{D_n}$ lze její obecné řešení vyjádřit jako \begin{equation} \Delta n = A \exp\left(-\frac{x}{L_n}\right) + B \exp\left(\frac{x}{L_n}\right) - \frac{\beta K I \tau_n}{K^2 L_n^2 - 1} \exp(-Kx). \end{equation} Konstanty $A$, $B$ se určují z okrajových podmínek. Na povrchu fotočlánku je povrchová rekombinace s rychlostí rekombinace elektronů $s_n$ \begin{equation} D_n \left. \frac{\mathrm{d} \Delta n}{\mathrm{d}x} \right|_{x=0} = s_n \left. \Delta n \right|_{x=0}. \end{equation}
Na hranici OPN ($x = l_1$) dochází vlivem eleketrického pole k úplnému odsátí nosičů náboje, a platí tedy \begin{equation} \left. \Delta n \right|_{x=l_1} = 0. \end{equation} Určením konstant $A, B$ získáme závislost koncentrace $\Delta n(x)$ a vypočteme hustotu elektronového proudu na hranici OPN \begin{equation} \left. J_n \right|_{l_1} = \left. e D_n \frac{\mathrm{d} \Delta n}{\mathrm{d} x} \right|_{l_1}. \end{equation} Podobně se počítá příspěvek proudu z části N, kde okrajové podmínky jsou \begin{equation} \left. \Delta p \right|_{x=l_2} = 0, \left. \Delta p \right|_{x\to\infty} = 0. \end{equation} Předpokládáme, že šířka oblasti N je velká proti $L_p$. Hustota děrového proudu na hranici OPN je \begin{equation} \left. J_p \right|_{l_2} = \left. -e D_p \frac{\mathrm{d} \Delta p}{\mathrm{d} x} \right|_{l_2}. \end{equation} Pro generaci $G$ v oblasti OPN platí \begin{equation} G = \beta K I \exp(-K l_1) \exp(-K(x-l_1)). \end{equation} Proudová hustota je \begin{equation} J(\mathrm{OPN}) = \int_{l_1}^{l_2} e \beta K I \exp(-K l_1) \exp(-K(x-l_1)) \,\mathrm{d}x. \end{equation} Celková hustota světlem generovaného proudu $J_L$ je součtem všech tří příspěvků a explicitní výraz pro ni lze nalézt např. v [2; 3].
Zatěžovací charakteristika
Pro pochopení funkce fotočlánku je vhodné vycházet z náhradního schématu podle Obr. 4, kde je osvětlený přechod představován generátorem proudu $J_\mathrm{L}$ s paralelně připojenou diodou. Je nutno počítat s určitým sériovým ($R_\mathrm{s}$) a paralelním ($R_\mathrm{sh}$) odporem. Odpor $R_\mathrm{s}$ náleží neutrálním oblastem a zahrnuje také případnou nedokonalost kontaktů. Paralelní odpor souvisí obvykle se svody.
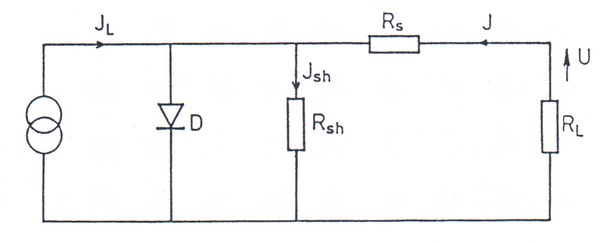
Proud $J_\mathrm{L}$ se dělí na proud diodou, paralelním odporem a zátěží $R_\mathrm{L}$. Proud zátěží $J$ se rovná \begin{equation} J = J_0 \left(\exp\left[\frac{e (U - J R_\mathrm{s})}{n k T}\right] - 1\right) + \frac{U - J R_\mathrm{s}}{R_\mathrm{sh}} - J_\mathrm{L}. \end{equation} Zde $n$ označuje faktor kvality diody (obvykle mívá hodnotu 1 až 2 podle způsobu přenosu náboje diodou) a $J_0$ je nasycený proud tekoucí v závěrném směru.
V ideálním případě, kdy neuvažujeme odpory $R_\mathrm{s}$ a $R_\mathrm{sh}$ ani vliv osvětlení na mechanizmus přenosu náboje, bude \begin{equation} \label{J} J = J_0 \left(\exp\left[\frac{e U}{n k T}\right] - 1\right) - J_\mathrm{L}. \end{equation} Z tohoto vztahu lze vypočítat tak zvané napětí naprázdno $U_{0\mathrm{C}}$, je-li $J = 0$ \begin{equation} U_{0\mathrm{C}} = \frac{n k T}{e} \ln(1 + \frac{J_L}{J_0}). \end{equation}
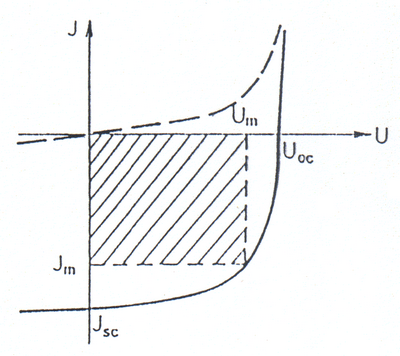
VA charakteristika osvětleného článku se bude podle $\eqref{J}$ lišit od temné jen posunutím podél proudové osy o hodnotu $J_L$ (viz Obr. 5). Část charakteristiky, která leží ve 4. kvadrantu, odpovídá režimu, kdy lze z vnějšího obvodu odebírat výkon a nazývá se zatěžovací charakteristikou. Na této křivce jsou důležité body $U_\mathrm{OC}$ (napětí naprázdno) a $J_\mathrm{SC}$ (proud nakrátko) a dále bod odpovídající maximálnímu výkonu, který lze z článku odebírat a jehož napěťová a proudová souřadnice je $U_\mathrm{m}$ a $J_\mathrm{m}$. Velikost maximálního výkonu je dána plochou největšího vepsaného obdélníku, jak je znázorněno na Obr. 5. Na základě toho se definuje faktor zaplnění $FF$ \begin{equation} FF = \frac{U_\mathrm{m} J_\mathrm{m}}{U_\mathrm{OC} J_\mathrm{SC}}. \end{equation} Maximální výkon $P_\mathrm{max} = J_\mathrm{SC} U_\mathrm{OC} FF$ a účinnost článku je pak $P_\mathrm{max}/P$, kde $P$ je výkon dopadajícího světla. Faktor zaplnění, napětí naprázdno a proud nakrátko udávají kvalitu fotočlánku.
Všimněme si, jakým způsobem ovlivní přítomnost $R_\mathrm{s}$ a $R_\mathrm{sh}$ zatěžovací charakteristiku. Obr. 6 naznačuje, že velký sériový odpor snižuje proud nakrátko a nízký paralelní odpor snižuje napětí naprázdno. Je zřejmé, že tím klesá faktor zaplnění [3].
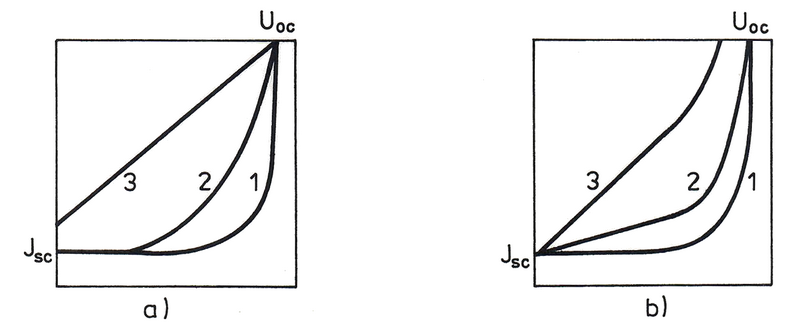
a) sériovým odporem 1: $R_\mathrm{s} = 0$; 2: $R_\mathrm{s} \in (0,\infty)$; 3: $R_\mathrm{s} \to \infty$
b) paralelním odporem 1: $R_\mathrm{sh} = \infty$; 2: $R_\mathrm{sh} \in (0,\infty)$; 3: $R_\mathrm{sh} \to 0$
Materiály pro sluneční články
Anorganické materiály
V praxi je stále nejvíce využíván křemík, a to v podobě monokrystalické, polykrystalické, nebo amorfní. Výhodou je, že se ho v zemské kůře nachází dostatek, není toxický a technologie výroby článků i celých panelů je již zvládnutá. Na druhé straně krystalický křemík má nízkou absorpci slunečního záření, což vede k nutnosti použití alespoň 200 mikrometrů tlustých destiček, a tedy k velké spotřebě materiálu, což se odráží i v ceně.
Jako určité řešení se jevil hydrogenizovaný amorfní křemík, který má velký absorpční koeficient, takže stačí jen několik mikrometrů tlustá vrstva k výrobě článků. Degradace vlivem slunečního záření je však vážnou překážkou a ke stabilizaci dochází až po roce provozu, po níž se účinnost ustaví na poměrně nízké hodnotě (10 %).
Články na základě heterogenního přechodu CdS/CdTe jsou stabilní. Technologie není náročná a spotřeba materiálu je poměrně nízká, neboť stačí jen asi 2 mikrometry tenké vrstvy. Námitkou je toxicita kadmia, která nevadí, pokud je článek zapouzdřený, ale problém může nastat při likvidaci. Nevýhodou jsou dále nízké zásoby teluru.
Kombinací Cu, In a Se jsou připravovány tenkovrstvé články s nízkou toxicitou a nenáročnou technologií.
Monokrystalické články z GaAs se uplatňují hlavně v kosmu vzhledem k odolnosti vůči radiaci a vysoké ceně.
Organické materiály
Sluneční články na bázi organických polovodičů, jejichž základem jsou molekuly, mají řadu výhod. Technologie jejich přípravy je poměrně jednoduchá, i když v posledních letech pro dosažení dostatečně velké účinnosti je třeba volit poněkud složitější postupy. Organické materiály lze nanášet z roztoku, což je energeticky málo náročné, např. oproti vakuovému napařování. Nejčastěji používané je rotační nanášení na skleněný substrát pokrytý vodivou vrstvou, která tvoří jednu z elektrod k aktivní vrstvě. Vlastnosti vrstev je možno měnit volbou koncentrace roztoku, a tloušťku vrstvy rychlostí otáček. Protože se tyto materiály vyznačují velkou absorpcí, stačí vytvořit tenké vrstvy o tloušťce 100–150 nanometrů, což znamená velkou úsporu materiálu a představuje další výhodu. V posledních letech byla vyvinuta levná metoda tisku vrstev na ohebný substrát, takže články lze získat i v rolích.
Organické články se nejčastěji vyrábějí z polymerů jako je poly(3-hexylthiofen) zkráceně P3HT, nebo z poly[(ethylhexyl-oxy)-benzodithiofen-(ethylhexyl)-thienothiogen] zkráceně PTB7 v kombinaci s deriváty fullerenu uváděnými jako PCBM, což jsou obvykle molekuly uhlíku C60.
Perovskity
V posledních letech se do popředí dostává materiál zvaný perovskit, který má krystalovou strukturu jako oxid titaničito-vápenatý (CaTiO3). Ve fotovoltaických článcích se však používá chemicky jiná látka, která se popisuje jako organicko-anorganický perovskit např. CH3NH3PbI3 s anorganickou mřížkou PbI3- obsahující uvnitř buněk organické molekuly CH3NH3+. Články dosáhly účinnosti 19,1 %. Problémem je však nestabilita a obsah olova v článcích. Složitější struktury na bázi perovskitů už vykazují účinnost 25 % [4]. Kombinací širokopásových a úzkopásových článků byly vyrobeny výhradně perovskitové tandemové články s účinností téměř 25 %. Pokud by se podařilo vyrábět moduly ve velkém, mohly by konkurovat křemíkovým. Perspektivní jsou také tandemy s krystalickým křemíkem nebo např. s CuInSe2.
Literatura ke studijnímu textu
- Lorenzo, Eduardo et al. Solar Elektricity: Engineering of Photovoltaic System. Madrid: Progensa, 1994. ISBN 84-86505-55-0.
- Hovel, H. J. Semiconductors and Semimetals. Vol. 11, Solar Cells. 1975.
- Green, M. A. Solar Cells. Englewood Clifs: Printice-Hall, 1982.
- Cao, F., Bian, L., Li, l. Perovskite solar cells with high-efficiency exceeding 25%: A review. Energy Materials and Devices, 2024, vol. 2, no. 1, s. 9370018. https://doi.org/10.26599/EMD.2024.9370018.