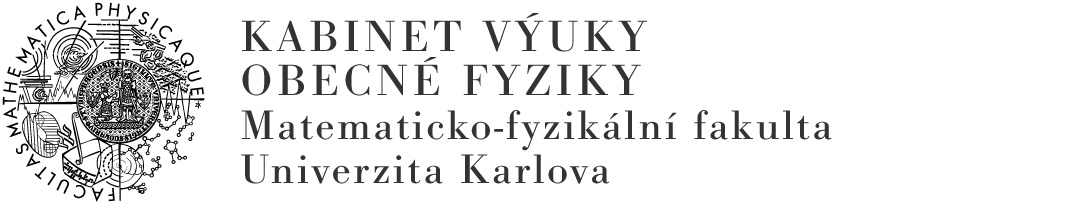K vysvětlení ohybového jevu použijeme Fraunhoferovu teorii, ve které se předpokládá, že dopadající vlna na štěrbinu je rovinná (viz Obr. 1). Ohybové jevy se nazývají Fraunhoferovy a pro potřeby praktika je vysvětleme jen na základě elementárních představ z Obr. 1.
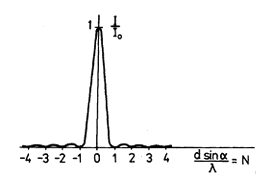
Předpokládejme, že rovinná monochromatická a koherentní vlna dopadá na jedinou štěrbinu šířky $d = \left\lvert AC \right\rvert$ a ohýbá se o úhel $\alpha$ definující náhodně vybraný směr (viz Obr. 1). Jestliže by se vzdálenost $\left\lvert BC \right\rvert$ rovnala právě vlnové délce $\lambda$, pak úsudkem lehce zjistíme, že součet intenzit elektrického pole od všech paprsků (elmg. záření), které ze štěrbiny vystupují v tomto směru, je nulový, jinými slovy se tyto paprsky navzájem vyruší. Každému paprsku mezi paprsky 1 a 2 odpovídá totiž paprsek z druhé poloviny štěrbiny 2 až 3, který se od něho liší právě o dráhový rozdíl $\lambda/2$, takže se s ním interferencí zruší (takovou dvojici představují např. paprsky 1 a 2, přičemž paprsky 1 a 3 jsou limitně blízko ke kraji štěrbiny a jeden z nich nevykompenzovaný díky limitě nehraje roli). Proto, uvážíme-li platnost vztahu $\left\lvert BC \right\rvert = d \cdot \sin\alpha$ a připustíme-li i jiný nenulový celočíselný násobek vlnové délky $\lambda$, dostaneme úvahou podmínku pro polohu minim $\eqref{min}$. Exaktním řešením ohybového jevu, které není pro potřeby praktika nutné, pak získal Fraunhofer rozložení intenzity prošlého záření s hlavním maximem a řadou postranních maxim a minim (Obr. 2).
Tuto intenzitu prošlého záření je možno vyjádřit jako funkci úhlu $\alpha$ \begin{equation} \label{Ialpha} I(\alpha) = I(0) \cdot \left[\frac{\sin \beta}{\beta} \right]^2, \end{equation} kde \begin{equation} \label{beta} \beta = \frac{\uppi d}{\lambda} \sin \alpha. \end{equation}
Z rovnice $\eqref{Ialpha}$ vyplývají následující závěry. Poloha minim intenzity je ve směrech, kde je splněna podmínka \begin{equation} \label{min} \frac{I(\alpha)}{I(0)} = 0 \Rightarrow \frac{\sin\beta_{\mathrm{min}}}{\beta_{\mathrm{min}}} = 0 \Rightarrow \beta_{\mathrm{min}} = n\uppi, n \in \mathbb{N}^{+} \end{equation} neboli podmínka pro úhly $\alpha_{\mathrm{min}}$, pro které nastává minimum, je \begin{equation} \label{alphamin} \alpha_{\mathrm{min},\,n} = \arcsin \left(\frac{n \lambda}{d} \right), n \in \mathbb{N}^{+}. \end{equation}
Poloha maxim intenzity (tj. $I(\alpha)/I(0)$ je maximální) je pak v místech, kde je splněna podmínka \begin{equation} \label{max} \frac{\mathrm{d}I}{\mathrm{d}\beta} = 0 \Rightarrow \tan \beta_{\mathrm{max}} = \beta_{\mathrm{max}}, \end{equation} což platí pro \begin{equation} \label{betamax} \begin{split} \beta_{\mathrm{max},\,1} = 4{,}4925&; \beta_{\mathrm{max},\,2} = 7{,}7252;\\ \beta_{\mathrm{max},\,3} = 10{,}901&; \beta_{\mathrm{max},\,4} = 14{,}071 \ldots, \end{split} \end{equation} neboli podmínka pro úhly $\alpha_{\mathrm{max}}$, při kterých nastává maximum, je \begin{equation} \label{alphamax} \begin{split} \alpha_{\mathrm{max},\,1} = \arcsin \left(\frac{4{,}4925 \lambda}{\uppi d} \right)&; \alpha_{\mathrm{max},\,2} = \arcsin \left(\frac{7{,}7252 \lambda}{\uppi d} \right);\\ \alpha_{\mathrm{max},\,3} = \arcsin \left(\frac{10{,}901 \lambda}{\uppi d} \right)&; \alpha_{\mathrm{max},\,4} = \arcsin \left(\frac{14{,}071 \lambda}{\uppi d} \right)\ldots \end{split} \end{equation}
Relativní velikost maxim intenzity v místech, kde je splněna podmínka $\eqref{alphamax}$, je \begin{equation} \label{Imax} \begin{split} \left(\frac{I(\alpha)}{I(0)}\right)_{\mathrm{max},\,1} = 0{,}0472&; \left(\frac{I(\alpha)}{I(0)}\right)_{\mathrm{max},\,2} = 0{,}0165;\\ \left(\frac{I(\alpha)}{I(0)}\right)_{\mathrm{max},\,3} = 0{,}00834&; \left(\frac{I(\alpha)}{I(0)}\right)_{\mathrm{max},\,4} = 0{,}00503\ldots \end{split} \end{equation}