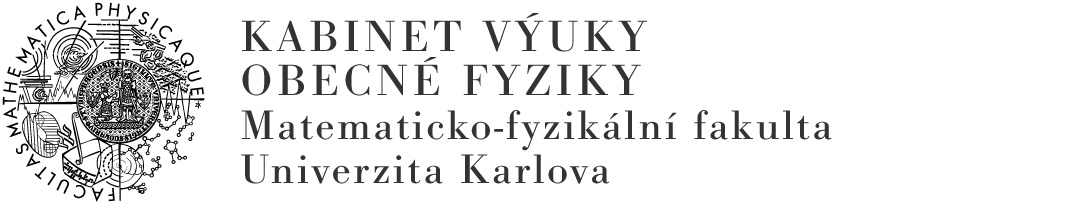Usměrňovače napětí

Žijeme ve světě střídavých a stejnosměrných proudů. Střídavý proud se nejvíce využívá při přenosu elektrické energie. Avšak spotřební elektronika a některá další elektrická zařízení (používaná např. v dopravních prostředcích nebo průmyslových aplikacích) jsou napájena výhradně ze stejnosměrných zdrojů. Proto je součástí většiny elektrických přístrojů a zařízení spotřební elektroniky usměrňovač. Usměrňovače jsou elektronické obvody, které umožňují přeměnu střídavého elektrického proudu na proud stejnosměrný.

Historicky byly nejdříve usměrňovače rtuťové, elektronkové, selenové, později polovodičové. Budeme se zabývat klasickými polovodičovými usměrňovači jednocestnými a dvoucestnými. V poslední době jsou ve zdrojích používané usměrňovače řízené, spínané. Zmíníme zde spínané zdroje, tzv. měniče napětí, které pracují s vyšší frekvencí, než je frekvence sítě 50 Hz (řádově kHz). Tyto moderní zdroje dosahují vysoké účinnosti, malých rozměrů, nízkých výrobních nákladů aj.

V této úloze se seznámíme s činností usměrňovačů a filtrů a se vztahy mezi střední, efektivní a špičkovou hodnotou napětí.

Střední hodnota napětí

Pokud je napětí časově nezávislé, je jeho střední hodnota rovna okamžité hodnotě. Mění-li se periodicky s časem, je střední hodnota definována vztahem \begin{equation} U_{\mathrm{e}} = \frac{1}{T} \int_0^T u(t) \,\mathrm{d}t, \end{equation} ve kterém $u(t)$ je okamžitá hodnota napětí v čase $t$ a $T$ je doba jedné periody.

Na stejnosměrných rozsazích analogových i digitálních měřicích přístrojů měříme vždy střední hodnotu. Při periodicky se měnícím signálu je údaj přístroje časově nezávislý, pokud doba kmitu $T$ signálu je podstatně menší než doba kmitu systému analogového přístroje, či doba jednoho měření digitálního přístroje – tzv. integrační doba (u ručních multimetrů zpravidla pevně daná ve stovkách ms). Při velmi pomalu se měnícím signálu údaj měřicího přístroje sleduje okamžité hodnoty. Je-li průběh signálu sinusový, je údaj měřicího přístroje na stejnosměrném rozsahu nulový, pokud frekvence signálu je dostatečně vysoká. Za dostatečně vysokou frekvenci je možno považovat frekvenci elektrické sítě 50 Hz.

Efektivní hodnota napětí

Efektivní hodnota napětí $U$ souvisí s okamžitou hodnotou napětí $u(t)$ integrálním vztahem \begin{equation} \label{Uef} U^2 = \frac{1}{T} \int_0^T u^2(t) \,\mathrm{d}t, \end{equation} ve kterém je opět $T$ perioda a $t$ čas.

Je-li závislost napětí na čase harmonická, tedy $u(t)=U_0\sin(\omega t + \phi)$, plyne ze vztahu $\eqref{Uef}$, že platí \begin{equation} \label{harm} U = \frac{U_0}{\sqrt{2}}, \end{equation} kde $U_0$ vyjadřuje amplitudu střídavého napětí.

Výchylka měřicích přístrojů s elektromagnetickým či elektrodynamickým systémem je úměrná efektivní hodnotě proudu, který systémem protéká. U běžně používaných přístrojů s otočnou cívkou či u přístrojů digitálních (elektronických) je výchylka úměrná střední hodnotě proudu. Při měření na střídavých rozsazích se musí signál nejprve usměrnit. Výchylka je potom úměrná střední hodnotě usměrněného proudu. Stupnice je však udělána tak, abychom při harmonickém průběhu signálu mohli přímo číst efektivní hodnoty. Jestliže průběh signálu není harmonický, neodpovídá údaj měřicího přístroje efektivním hodnotám. Protože odečtené napětí na přístroji není v tomto případě efektivní hodnotou, nevyhovuje tento údaj vztahu $\eqref{Uef}$, a pochopitelně ani vztahu $\eqref{harm}$.

RMS a True RMS měřicí přístroje

Efektivní hodnota bývá často označována jako RMS (z angličtiny Root Mean Square, doslovně česky odmocnina průměru čtverců). Elektrická síť v Česku má v jednofázové síti napětí 230 V (efektivní hodnota, tj. maximální hodnota napětí je 325 V) a frekvenci 50 Hz. Efektivní hodnota sdruženého napětí ve třífázové síti je 400 V.

Jednodušší měřicí přístroje, které se běžně používají, měří přesně efektivní hodnotu pouze ze standardních sinusových průběhů. Přesné měřicí přístroje, které měří efektivní hodnotu i z nesinusových vlnových průběhů střídavého napětí nebo proudu, se nazývají True RMS. Toto označení bývá uvedeno na měřicím přístroji.

Jednocestný usměrňovač

Zapojení jednocestného usměrňovače s odporovou zátěží je na Obr. 1. Transformované střídavé napětí je usměrněno jednou diodou.

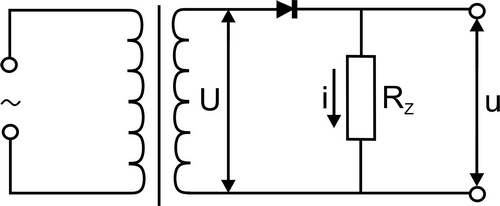
Na primární vinutí transformátoru je zapojeno střídavé napájecí napětí, zpravidla ze sítě. V sekundárním vinutí se indukuje střídavé napětí $U$, jehož průběh je na Obr. 2a. Usměrňovač propustí proud do zátěže R_Z pouze tehdy, je-li na horní straně transformátoru kladná půlvlna střídavého napětí. Na zatěžovacím rezistoru vznikne průtokem tohoto proudu $I$ napětí pouze po dobu trvání kladné půlvlny na horním vývodu transformátoru. Při záporné půlvlně bude spád napětí na zatěžovacím rezistoru nulový. Průběh tohoto usměrněného napětí je zakreslen na Obr. 2b. Střední hodnota jednocestně usměrněného harmonického napětí souvisí se špičkovou hodnotou podle vztahu \begin{equation} U_{\mathrm{e}} = \frac{U_0}{\pi}. \end{equation}

Dvoucestný usměrňovač

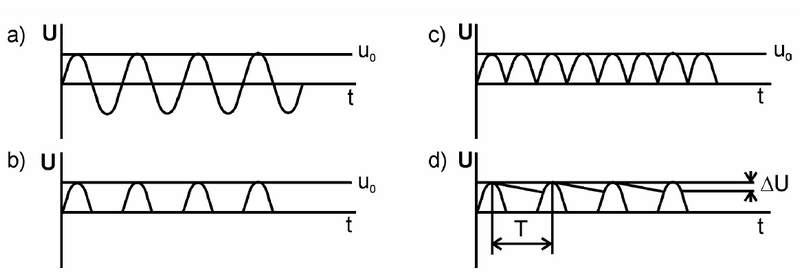
Dvoucestný usměrňovač propouští obě půlvlny vstupního napětí. Tohoto chování lze dosáhnout například pomocí Graetzova obvodu (viz Obr. 3) využívajícího můstkového zapojení čtyř diod.

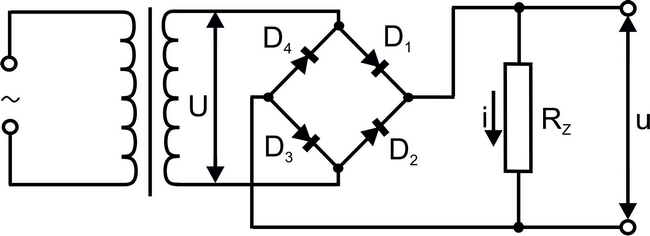
Činnost můstkového usměrňovače je následující. Pokud má horní uzel sekundárního vinutí transformátoru vyšší potenciál než uzel spodní, teče proud $i$ od horního uzlu transformátoru přes diodu D₁, zatěžovací rezistor R_Z a diodou D₃ k dolnímu uzlu transformátoru. Diody D₂ a D₄ jsou zavřené. Změní-li se polarita napětí na sekundárním vinutí transformátoru, teče proud $i$ od dolního uzlu transformátoru přes diodu D₂, zatěžovací rezistor R_Z a přes diodu D₄ k hornímu uzlu. Směr proudu v zatěžovacím rezistoru bude v obou půlperiodách stejný. Průběh napětí $u$ na zátěži je zakreslen na Obr. 2c. V obou těchto případech je střední hodnota usměrněného napětí \begin{equation} U_{\mathrm{e}} = \frac{2}{\pi} U_0. \end{equation}

Usměrňovače ve spínaných zdrojích

Moderní stejnosměrné zdroje obsahují tzv. spínaný zdroj. Spínaný zdroj osahuje spínací prvek, který je spínán vysokou frekvencí, resp. je též spínán na základě zpětné vazby, aby usměrněné napětí mělo konstantní velikost i při proměnné zátěži. Na rozdíl od lineárních zdrojů (zdroje pouze s usměrňovačem a pracující na síťové frekvenci 50 Hz) jsou mnohem účinnější a lehčí, protože zpravidla pracují s vysokou spínací frekvencí, díky níž lze použít menší transformátory s feritovými jádry a menší filtrační kondenzátory. Se spínanými zdroji se lze setkat v nabíječkách mobilních telefonů, v noteboocích, ve zdrojích osobních počítačů aj. V současné době se lineární zdroje používají spíše v laboratořích, kde je ceněno malé zvlnění rušení.

Princip spínaných zdrojů je následující. Napětí z rozvodné sítě 230 V / 50 Hz se nejdříve usměrní pomocí usměrňovacího můstku a vyhladí na vstupním kondenzátoru. Pak se toto stejnosměrné napětí (cca 325 V) „rozseká“ pomocí spínacích tranzistorů na pulzy (frekvence spínání řádově desítky kHz). Toto pulzní napětí je přivedeno na primární vinutí transformátoru s feritovým jádrem, který zpětně transformuje vysoké pulzy na nízké pulzy přibližně o velikosti požadovaného malého stejnosměrného napětí. Na sekundární straně tohoto transformátoru jsou pulzy opět usměrněny pomocí můstkového usměrňovače a poté ještě vyhlazeny kondenzátorem. U precizních spínaných zdrojů se o stabilitu výstupního napětí stará zpětná vazba, která je zavedena z výstupu do vstupu a řídí frekvenci spínání.

Filtrace usměrněného napětí

Usměrněné napětí z diod je na zatěžovacím rezistoru R_Z pulzující. Toto napětí můžeme vyhladit (filtrovat), připojíme-li k němu paralelně kondenzátor o kapacitě $C$ (viz Obr. 4 a Obr. 5). Pokud by byl odpor $R_\mathrm{z}$ nekonečně velký, nabil by se tento kondenzátor na špičkovou hodnotu usměrněného napětí a napětí na kondenzátoru by zůstalo konstantní. Má-li však odpor $R_\mathrm{z}$ konečnou hodnotu, vybíjí se kondenzátor C přes rezistor R_Z s časovou konstantou $R_\mathrm{z}C$.

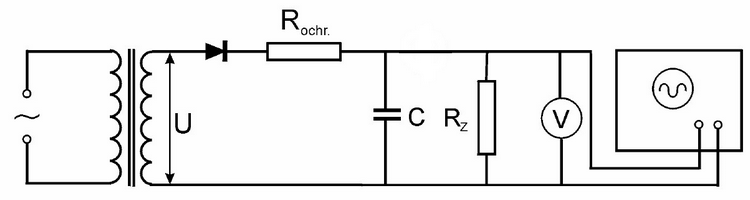
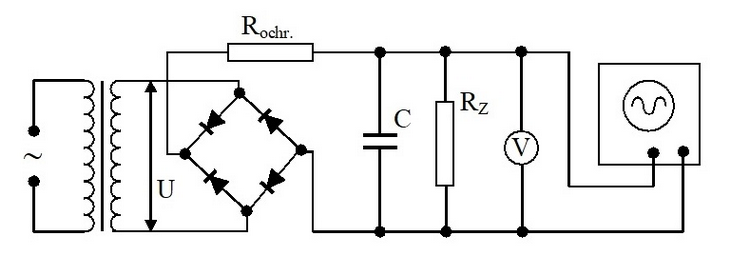
V čase mezi následujícími dvěma pulzy bude probíhat pokles napětí na kondenzátoru. Časový průběh napětí $u$ na rezistoru R_Z je roven \begin{equation} \label{U0} u = U_0 \exp{\left(-\frac{t}{R_{\mathrm{z}}C}\right)}, \end{equation} je-li $U_0$ špičková hodnota napětí, na které se nabije kondenzátor, a $t$ čas. Kondenzátor C se vybíjí přes rezistor R_Z až do příchodu následujícího pulzu. Pak se začne nabíjet na špičkovou hodnotu. Pokud by zdroj, reprezentovaný sekundárním vinutím transformátoru a diodou, měl nulový vnitřní odpor, sledoval by průběh napětí na kondenzátoru náběžnou hranou pulzu. Tento předpoklad však není splněn, a kromě toho se zařazuje mezi diodu a zatěžovací obvod (viz Obr. 4 a Obr. 5) ochranný rezistor. Zapojením tohoto rezistoru se má zabránit přetížení zdroje při počátečním nabíjení kondenzátoru. Kondenzátor se proto nabije přes rezistor o odporu $r$, který je roven součtu vnitřního odporu zdroje a odporu ochranného rezistoru. Velikost odporu $r$ musí být menší než velikost zatěžovacího odporu. Pak je časová konstanta nabíjení $rC$ menší než časová konstanta vybíjení $R_{\mathrm{z}}C$.

Výpočet časové závislosti napětí na zatěžovacím rezistoru je obecně složitý. Abychom výpočet zjednodušili, budeme předpokládat, že časová konstanta vybíjení $\tau_{\mathrm{v}} = R_{\mathrm{z}} C$ je podstatně delší než doba mezi po sobě následujícími pulzy (u jednocestného usměrnění doba periody kmitu $T$, u dvoucestného usměrnění $T/2$) a že doba, po kterou se kondenzátor nabíjí, je zanedbatelně krátká. Tyto předpoklady jsou poměrně dobře splněny, pokud činitel filtrace je velký. Činitel filtrace $k_{\mathrm{f}}$ je definován jako poměr špičkové hodnoty střídavého napětí $U_0$ na sekundárním vinutí transformátoru ku špičkové hodnotě střídavé složky usměrněného napětí $\Delta U$ (viz Obr. 2d) \begin{equation} k_{\mathrm{f}} = \frac{U_0}{\Delta U}, \end{equation} přičemž špičková hodnota střídavé složky usměrněného napětí $\Delta U$ je definovaná jako rozdíl minimální a maximální hodnoty napětí a označuje se zvlnění. Činitel zvlnění $k_{\mathrm{zv}}$ je pak definován jako převrácená hodnota z činitele filtrace $k_{\mathrm{f}}$.

Je-li změna napětí na kondenzátoru malá, lze průběh napětí na rezistoru R_Z mezi dvěma následujícími nabíjecími pulzy vyjádřit přibližně vztahem \begin{equation} u \cong U_0 \left(1-\frac{t}{R_{\mathrm{z}}C}\right), \end{equation} který získáme, rozložíme-li výraz $\eqref{U0}$ v řadu a vezmeme pouze prvé dva členy. V okamžiku, kdy přijde nabíjecí pulz, se kondenzátor nabije na napětí $U_0$. Zde činíme určité zjednodušení, neboť předpokládáme, že nabíjecí pulz je nekonečně krátký. Za dobu $t_0$, než přijde následující pulz, se kondenzátor vybije na hodnotu \begin{equation} u(t_0) = U_0 \left(1-\frac{t_0}{R_{\mathrm{z}}C}\right). \end{equation} Pro jednocestný usměrňovač, u kterého je $t_0 \cong T$ ($T$ je perioda kmitu), bude činitel filtrace roven \begin{equation} \label{kfhw} k_{\mathrm{f}} = \frac{U_0}{U_0-u(t_0)} = \frac{R_{\mathrm{z}}C}{T}. \end{equation} Při dvoucestném usměrnění, kdy $t_0 = T/2$, bude \begin{equation} \label{kffw} k_{\mathrm{f}} = \frac{2 R_{\mathrm{z}}C}{T}. \end{equation} Je zřejmé, že při dvoucestném usměrnění postačí k dosažení daného koeficientu filtrace poloviční filtrační kapacita $C$ ve srovnání s usměrňovačem jednocestným.

Ze vztahů $\eqref{kfhw}$ a $\eqref{kffw}$ plyne, že pro udržení daného činitele filtrace je nutno při změně zatěžovacího proudu, tj. změně proudu odebíraného zátěží, změnit filtrační kapacitu tak, aby časová konstanta zatěžovacího obvodu zůstávala konstantní. Proud zátěží, který označíme $I_{\mathrm{ss}}$, je s odporem $R_{\mathrm{z}}$ svázán Ohmovým zákonem \begin{equation} \label{Iss} I_{\mathrm{ss}} = \frac{U_{\mathrm{ss}}}{R_{\mathrm{z}}}, \end{equation} ve kterém $U_{\mathrm{ss}}$ je stejnosměrné napětí na zátěži. Pokud je činitel filtrace $k_{\mathrm{f}} \gg 1$, je $U_{\mathrm{ss}} = U_0$. Ze vztahů $\eqref{kfhw}$, $\eqref{kffw}$, $\eqref{Iss}$ vyplývá pro závislost filtrační kapacity na proudu odbíraném zátěží přibližný vztah (při $k_{\mathrm{f}} \gg 1$) \begin{equation} C = \frac{T k_{\mathrm{f}} I_{\mathrm{ss}}}{n U_0}. \end{equation} Veličina $n$ je přitom rovna jedné při jednocestném usměrnění a $n = 2$ při dvoucestném usměrnění.

Na závěr je třeba poznamenat, že výše uvedený způsob filtrace je nejjednodušší a nemá optimální parametry. V praxi se proto častěji setkáváme s filtry, které jsou sestaveny z tlumivky a kondenzátoru. U těchto filtrů lze snadněji dosáhnout vyšších hodnot činitele filtrace než u filtrů odporově kapacitních.

Literatura ke studijnímu textu

1. Brož, Jaroslav. Základy fyzikálních měření I, Praha: SPN, 1983. Stať 4.4.1.
2. Bakule, Roman a Šternberk, Jiří. Fyzikální praktikum II, Praha: Univerzita Karlova, 1989.